3. Feature Reduction

Once a meaningful set of time series features has been extracted for each variable and participant, the total number of data points sometimes remains too large for the desired clustering algorithm (Altman & Krzywinski, 2018). In such cases, it is often recommended to perform an (optional) feature reduction. The commmonly used feature reduction procedures can commonly be separated into feature selection and feature projection. We provide a more detailed discussion of the pros and cons of the different approaches. For this illustration we focus on feature projections, which have been popular because they are efficient, widely available, and applicable to a wide range of data types. That being said, because feature selection procedures have the benefit that they retain the interpretable feature labels directly and immediately indicate which features were most informative in the sample (Carreira-Perpiñán, 1997), we recommend users to carefully consider the most useful option for their use case.

It is important to note again that a feature reduction step is not always necessary. Especially methods such as k-means are well equipped to deal with relatively large data sets (Jain, 2010). It is important to check whether the full feature set leads to convergence issues or unstable cluster solutions. We go through the feature reduction steps as an exemplary illustration only.

Principal Component Analysis

We, specifically, selected the commonly used principal component analysis (PCA). PCAs have the distinct benefit that they are well-established within the psychometric literature (Jolliffe, 2011) and can broadly be applied to a wide variety of studies in an automatized manner (Abdi & Williams, 2010). As our aim is to present a general illustration that can also be adopted across use cases, we present the workflow using a PCA here but we encourage users to consider more specialized methods as well.

Running the PCA

To use the PCA with our extracted time series features, we focus on a transformed feature set where the features are standardized across participants to ensure that all features are weighted equally. This transformation was already calculated as part of the featureExtractor() function and we now save it as a data frame scaled_data.

scaled_data <- featFullImp$featuresImpZMat %>% select(ends_with(feature_selection))

We then enter the standardized features into the principal component analysis using the prcomp() function from the stats package (R Core Team, 2024).

res.pca <- prcomp(scaled_data, scale. = FALSE)
pca_summary <- summary(res.pca)

# extract explained variances
res.varExplained <- data.frame(
  Explained_Variance = cumsum(summary(res.pca)[["importance"]]['Proportion of Variance',]),
  Components = seq(1, length(cumsum(summary(res.pca)[["importance"]]['Proportion of Variance',])), 1)
)

The PCA uses linear transformations in such a way that the first component captures the most possible variance of the original data (e.g., by finding a vector that maximizes the sum of squared distances; see Jolliffe (2002), Abdi & Williams (2010)). The following components will then use the same method to iteratively explain the most of the remaining variance while also ensuring that the components are linearly uncorrelated (Shlens, 2014). In practice, this meant that the PCA decomposed the 72 features into 72 principal components but now (because of the uncorrelated linear transformations) the first few principal components will capture a majority of the variance (see Table 1).

# Creating a data frame to hold variance details
variance_df <- data.frame(
  Component = 1:length(pca_summary$sdev),
  `Standard Deviation` = pca_summary$sdev,
  `Proportion of Variance` = pca_summary$importance[2, ],
  `Cumulative Proportion` = pca_summary$importance[3, ]
)

# Producing the kable output
variance_df %>%
 kbl(.,
      escape = FALSE,
      booktabs = TRUE,
      label = "pca_summary",
      format = "html",
      digits = 2,
      linesep = "",
      col.names = c("Component", "Standard Deviation", "Proportion of Variance", "Cumulative Proportion"),
      caption = "PCA Component Summary") %>%
  kable_classic(
    full_width = FALSE,
    lightable_options = "hover",
    html_font = "Cambria"
  ) %>%
  scroll_box(width = "100%", height = "500px")
Table 1: Variance Decomposition
PCA Component Summary
Component Standard Deviation Proportion of Variance Cumulative Proportion
PC1 1 2.75 0.11 0.11
PC2 2 2.51 0.09 0.19
PC3 3 1.97 0.05 0.25
PC4 4 1.90 0.05 0.30
PC5 5 1.73 0.04 0.34
PC6 6 1.67 0.04 0.38
PC7 7 1.59 0.04 0.41
PC8 8 1.49 0.03 0.44
PC9 9 1.46 0.03 0.47
PC10 10 1.38 0.03 0.50
PC11 11 1.35 0.03 0.52
PC12 12 1.32 0.02 0.55
PC13 13 1.30 0.02 0.57
PC14 14 1.28 0.02 0.59
PC15 15 1.24 0.02 0.62
PC16 16 1.20 0.02 0.64
PC17 17 1.17 0.02 0.65
PC18 18 1.15 0.02 0.67
PC19 19 1.13 0.02 0.69
PC20 20 1.07 0.02 0.71
PC21 21 1.06 0.02 0.72
PC22 22 1.03 0.01 0.74
PC23 23 1.00 0.01 0.75
PC24 24 0.99 0.01 0.76
PC25 25 0.96 0.01 0.78
PC26 26 0.94 0.01 0.79
PC27 27 0.93 0.01 0.80
PC28 28 0.89 0.01 0.81
PC29 29 0.88 0.01 0.82
PC30 30 0.86 0.01 0.83
PC31 31 0.84 0.01 0.84
PC32 32 0.83 0.01 0.85
PC33 33 0.81 0.01 0.86
PC34 34 0.79 0.01 0.87
PC35 35 0.77 0.01 0.88
PC36 36 0.75 0.01 0.89
PC37 37 0.73 0.01 0.89
PC38 38 0.72 0.01 0.90
PC39 39 0.69 0.01 0.91
PC40 40 0.67 0.01 0.91
PC41 41 0.64 0.01 0.92
PC42 42 0.64 0.01 0.93
PC43 43 0.61 0.01 0.93
PC44 44 0.60 0.01 0.94
PC45 45 0.59 0.00 0.94
PC46 46 0.58 0.00 0.94
PC47 47 0.56 0.00 0.95
PC48 48 0.54 0.00 0.95
PC49 49 0.53 0.00 0.96
PC50 50 0.51 0.00 0.96
PC51 51 0.50 0.00 0.96
PC52 52 0.48 0.00 0.97
PC53 53 0.47 0.00 0.97
PC54 54 0.44 0.00 0.97
PC55 55 0.44 0.00 0.98
PC56 56 0.42 0.00 0.98
PC57 57 0.41 0.00 0.98
PC58 58 0.40 0.00 0.98
PC59 59 0.39 0.00 0.98
PC60 60 0.37 0.00 0.99
PC61 61 0.36 0.00 0.99
PC62 62 0.35 0.00 0.99
PC63 63 0.34 0.00 0.99
PC64 64 0.31 0.00 0.99
PC65 65 0.29 0.00 0.99
PC66 66 0.28 0.00 1.00
PC67 67 0.27 0.00 1.00
PC68 68 0.25 0.00 1.00
PC69 69 0.23 0.00 1.00
PC70 70 0.23 0.00 1.00
PC71 71 0.20 0.00 1.00
PC72 72 0.17 0.00 1.00

Component Selection

We can then decide how much information (i.e., variance) we are willing to sacrifice for a reduced dimensionality. A common rule of thumb is to use the principal components that jointly explain 70–90% of the original variance (Jackson, 2003). For our illustration, we chose a 80% of the cumulative percentage explained variance as the cutoff (i.e., cutoff_percentage)

cutoff_percentage <- 0.8
pca_cutoff <- min(which(cumsum(summary(res.pca)[["importance"]]['Proportion of Variance',]) >= cutoff_percentage))

This means that we select the first 27 principal components that explain 80% of the variance in the original 72 features (reducing the dimensionality by 62.50%).

fviz_eig(res.pca, 
         addlabels = TRUE, 
         choice = "variance",
         ncp = pca_cutoff,
         barfill = "#a6a6a6",
         barcolor = "transparent",
         main = "Scree Plot of Explained Variance per Principal Component",
         xlab = "Principal Components") +
         theme_Publication() +
  theme(text = element_text(size = 14, color = "#333333"),
        axis.title = element_text(size = 16, face = "bold", color = "#555555"),
        plot.title = element_text(size = 18, hjust = 0.5, face = "bold", color = "#444444"),
        legend.position = "none",
        panel.grid.minor = element_blank())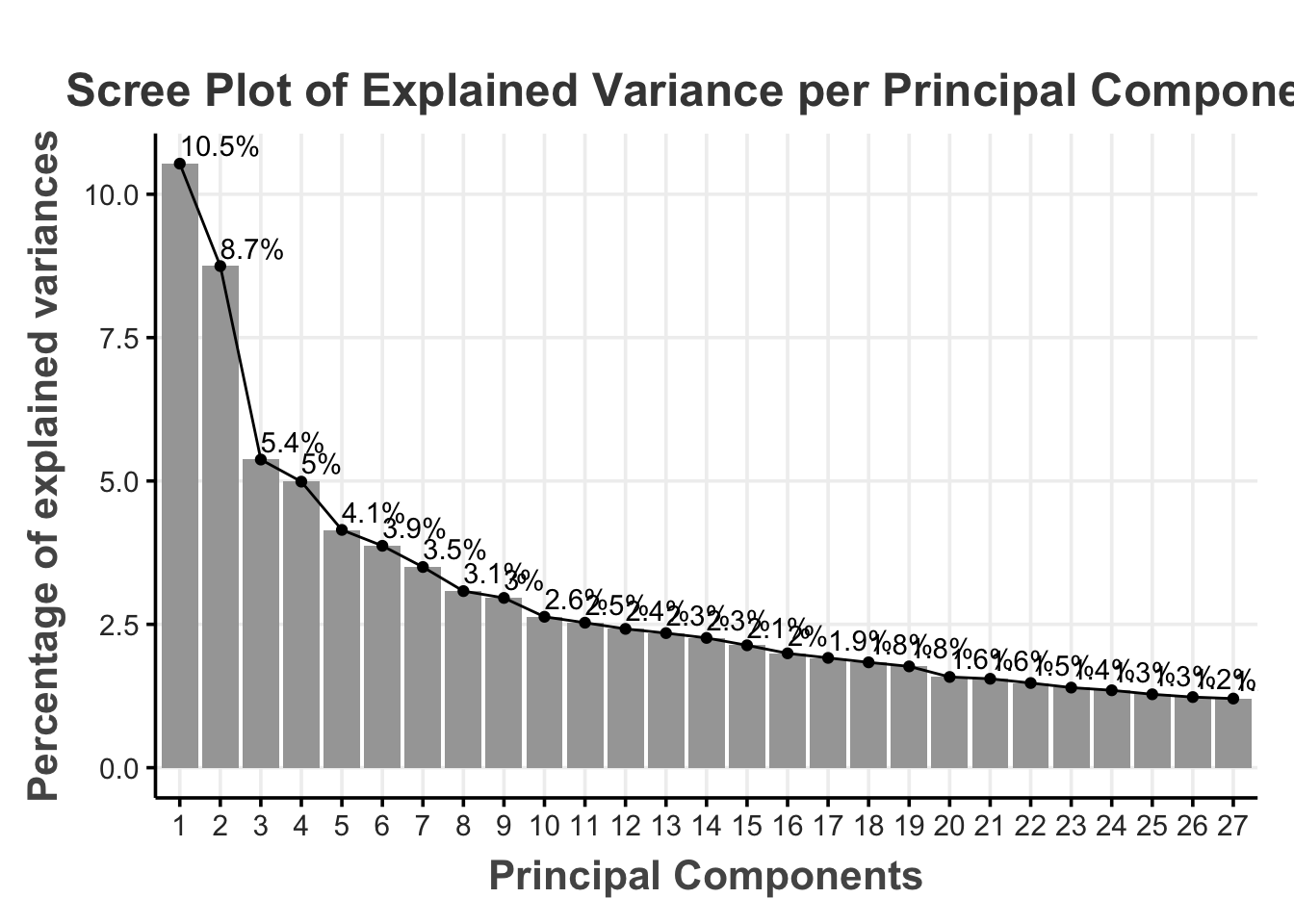

res.varExplained <- data.frame(
  Explained_Variance = cumsum(summary(res.pca)[["importance"]]['Proportion of Variance',]),
  Components = seq(1, length(cumsum(summary(res.pca)[["importance"]]['Proportion of Variance',])), 1)
)

ggplot(data = res.varExplained, aes(x = Components, y = Explained_Variance)) +
  geom_point() +
  geom_line() +
  geom_vline(mapping = aes(xintercept = pca_cutoff), linetype = "longdash") +
  geom_hline(mapping = aes(yintercept = cutoff_percentage), linetype = "longdash") +
  geom_text(aes(x = pca_cutoff, y = min(Explained_Variance) + 0.01), 
            label = paste0(pca_cutoff, " components"), hjust = -0.1, vjust = 0, size = 3) +
  geom_text(aes(x = min(Components), y = cutoff_percentage), 
            label = paste0(cutoff_percentage*100, "%"), hjust = 0, vjust = -1, size = 3) +
  labs(title = "Cumulative Proportion of Variance Explained",
       x = "Number of Components",
       y = "Proportion of Variance Explained") +
  tsFeatureExtracR::theme_Publication()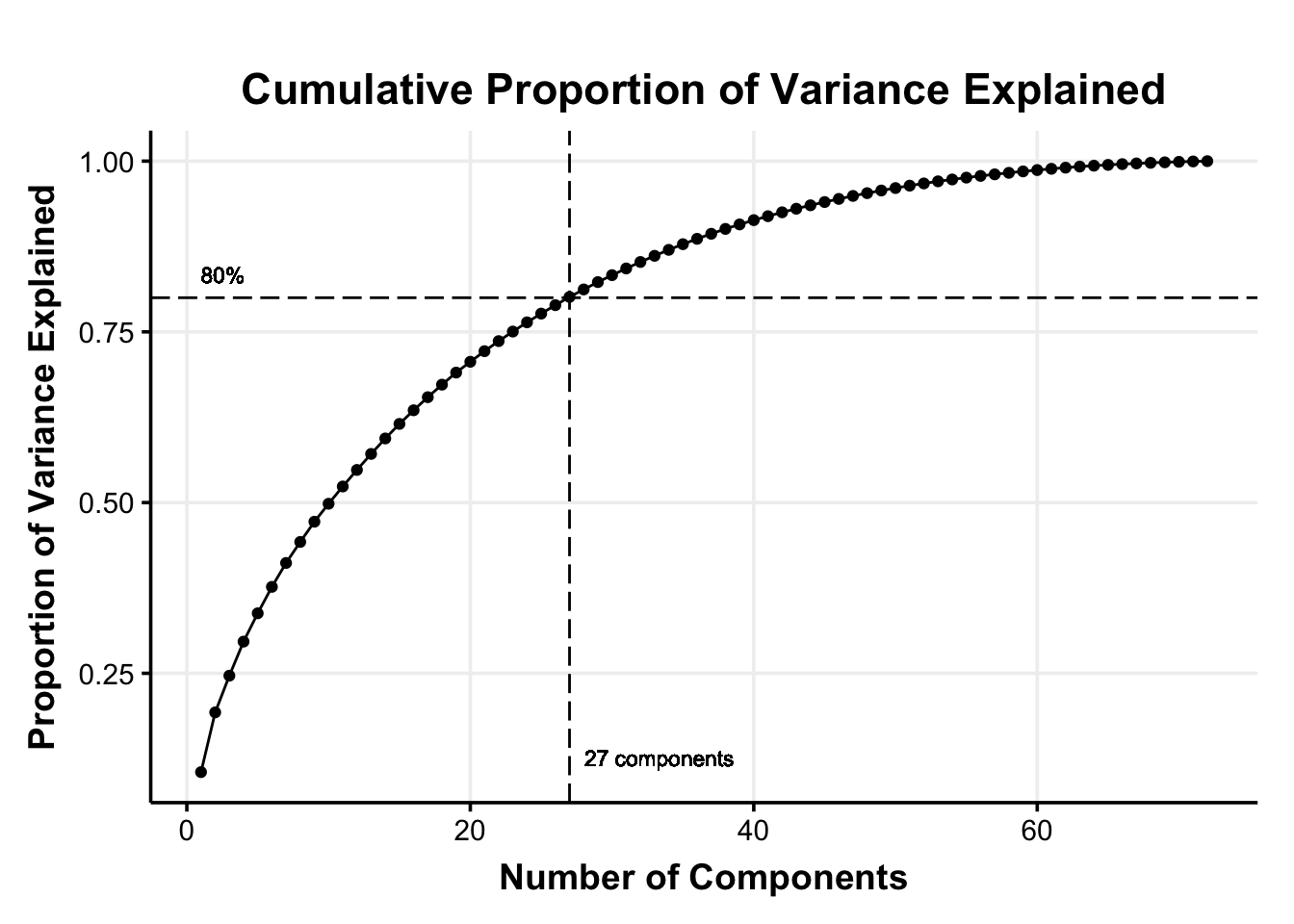

We can then also get a slightly better of an understanding of how the data is distributed by visualizing the features and the participants within the lower dimensional space. We here chose the first three principal components to allow for human undestandable dimensionality.

plot1 <- plot_ly(
  res.pca$rotation %>% as.data.frame,
  x = ~ PC1,
  y = ~ PC2,
  z = ~ PC3,
  size = 2,
  type = 'scatter3d',
  mode = 'markers',
  text = ~ paste('Variable:', rownames(res.pca$rotation))
) %>%
  layout(title = 'Variables in reduced space')
plot2 <- plot_ly(
  res.pca$x %>% as.data.frame,
  x = ~ PC1,
  y = ~ PC2,
  z = ~ PC3,
  size = 2,
  type = 'scatter3d',
  mode = 'markers',
  text = ~ paste('Participant:', rownames(res.pca$x))
) %>%
  layout(title = 'Participants in reduced space')

# Display side by side using htmltools
div(
  style = "display: flex; justify-content: space-between;",
  list(
    div(plot1, style = "width: 50%;"),
    div(plot2, style = "width: 50%;")
  )
)

Save Principal Component Scores

For the extracted principal components we save the 27 principal component scores for each participant (i.e., the participants’ coordinates in the reduced dimensional space; PC-scores) in the pca_scores data frame.

# extract coordinates for the individuals (PC-scores)
pca_scores <- as.data.frame(res.pca$x[,1:pca_cutoff])

It is important to note that we do not standardize the principal component scores again before adding them into the clustering algorithm. With the PCs the differences in variances are crucial to the dimensionality reduction and standardizing the PC-scores would remove this information.

pca_scores %>%
  summarize_all(sd) %>%
  pivot_longer(everything(), names_to = "PC", values_to = "sd") %>%
  ggplot(., aes(x=reorder(PC, sd), y=sd, label=sd)) +
  geom_bar(stat='identity', width=.5) +
  coord_flip() +
  labs(
    x = "Principal Component",
    y = "Standard Deviation",
    title = "Standard Deviation of each Principal Component"
  ) +
  theme_Publication()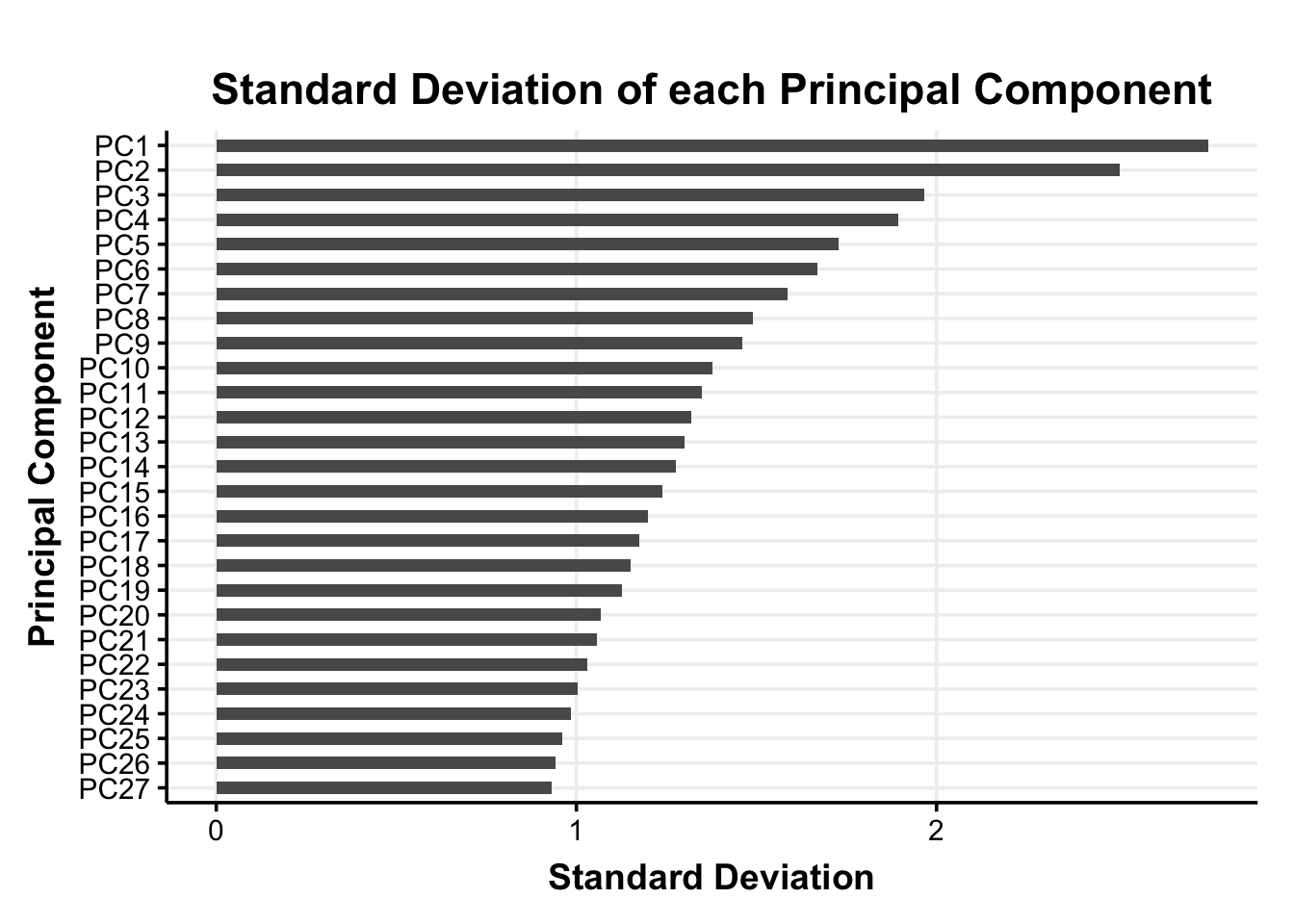

With the reduced variable space of the PC-scores we can now move on to the clustering of the data.

References

Abdi, H., & Williams, L. J. (2010). Principal component analysis: Principal component analysis. Wiley Interdisciplinary Reviews: Computational Statistics, 2(4), 433–459. https://doi.org/10.1002/wics.101
Altman, N., & Krzywinski, M. (2018). The curse(s) of dimensionality. Nature Methods, 15(6), 397–397. https://doi.org/10.1038/s41592-018-0019-x
Carreira-Perpiñán, M. Á. (1997). A Review of Dimension Reduction Techniques (Technical {Report} CS-96-09). Dept. of Computer Science, University of Sheffield.
Jackson, J. E. (2003). A user’s guide to principal components. Wiley-Interscience.
Jain, A. K. (2010). Data clustering: 50 years beyond K-means. Pattern Recognition Letters, 31(8), 651–666. https://doi.org/10.1016/j.patrec.2009.09.011
Jolliffe, I. (2002). Principal component analysis. Springer.
Jolliffe, I. (2011). Principal Component Analysis. In M. Lovric (Ed.), International Encyclopedia of Statistical Science (pp. 1094–1096). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-04898-2_455
R Core Team. (2024). R: A language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org/
Shlens, J. (2014). A Tutorial on Principal Component Analysis. https://doi.org/10.48550/ARXIV.1404.1100